Breathtaking Tips About Are Curved Lines Exponential Excel Chart Connect Missing Data Points

Press [graph] to observe the graph of the exponential function along with the line for the specified value of f (x).

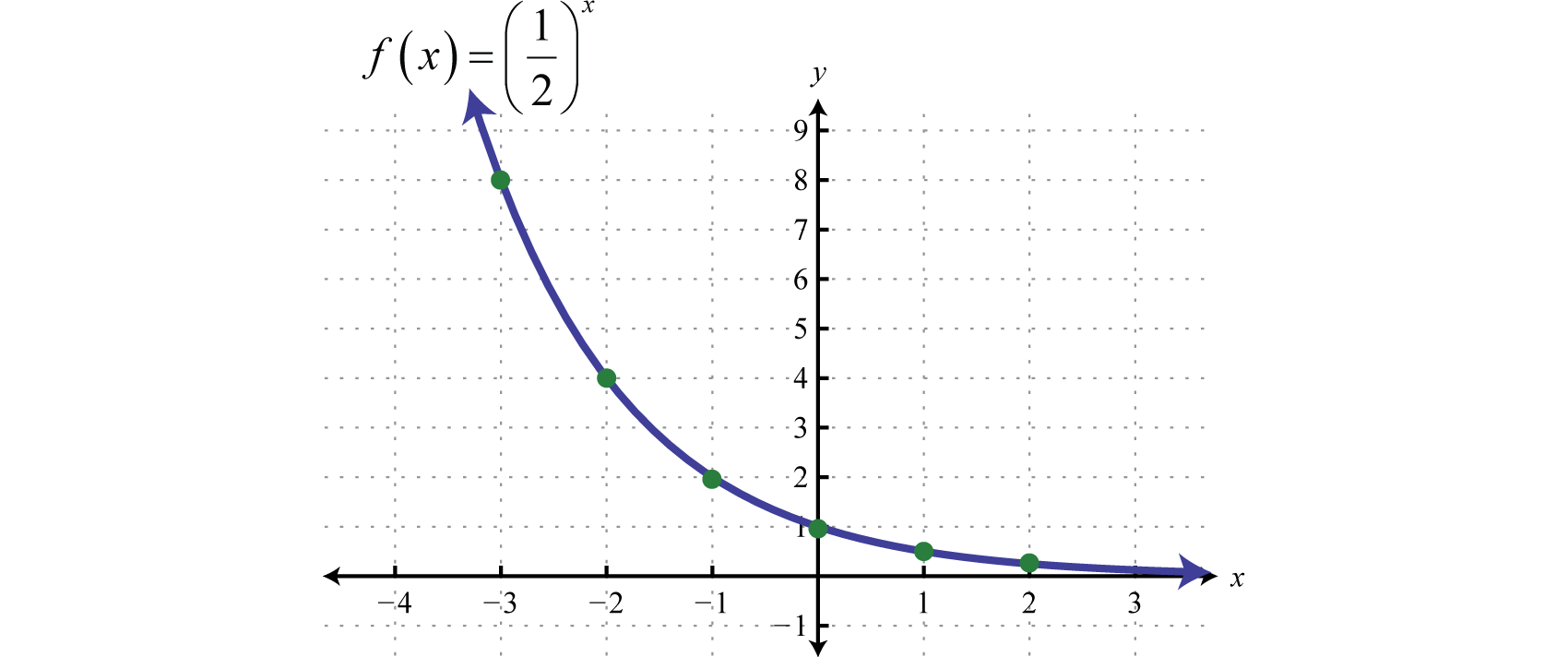
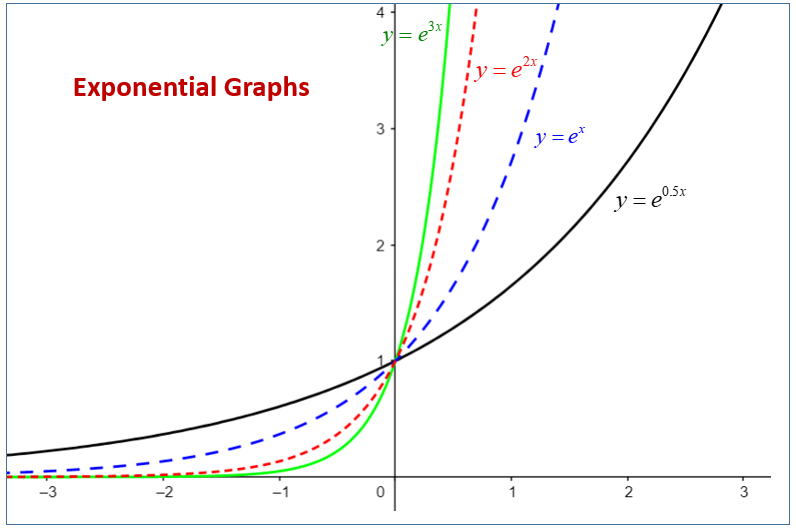
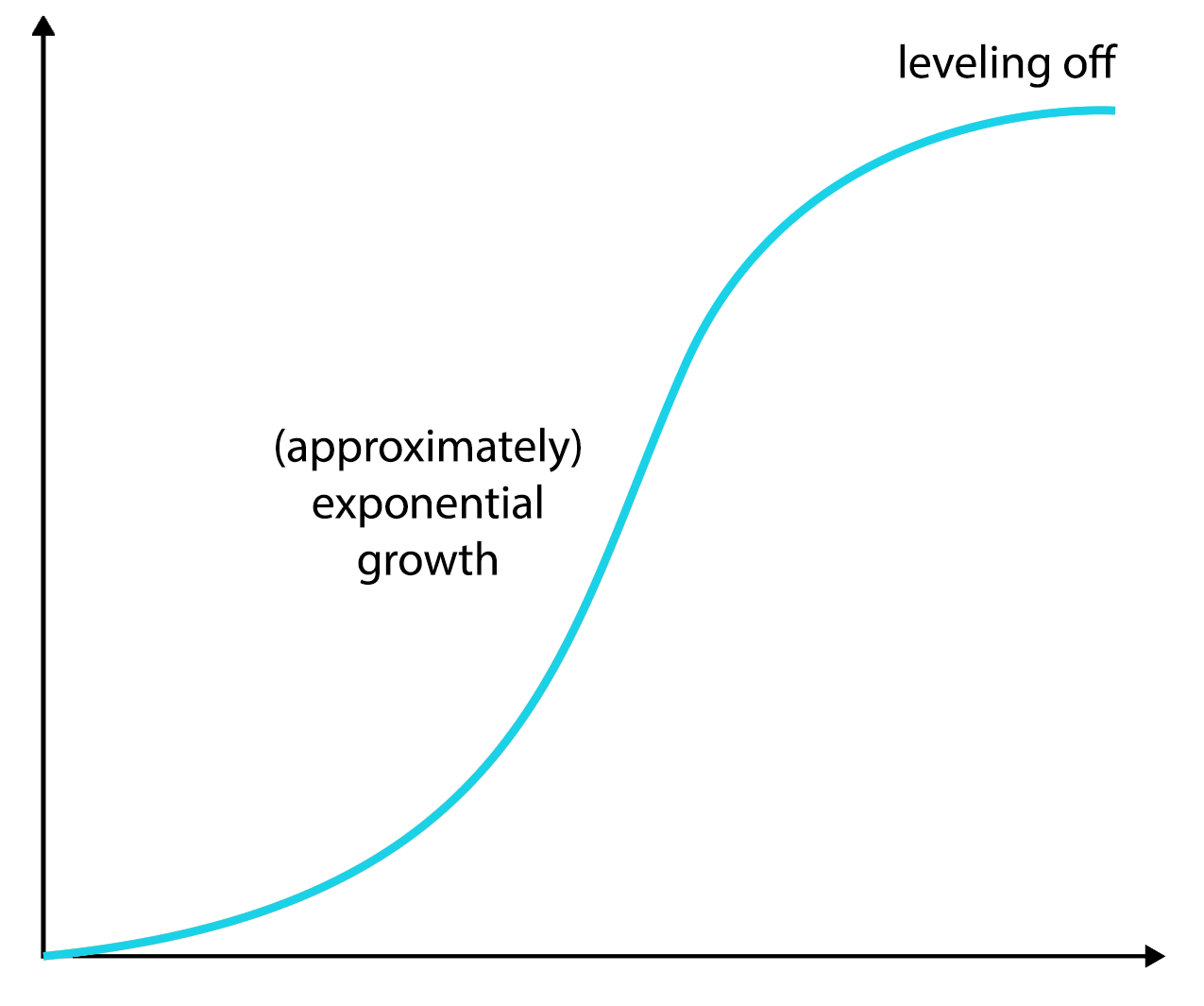
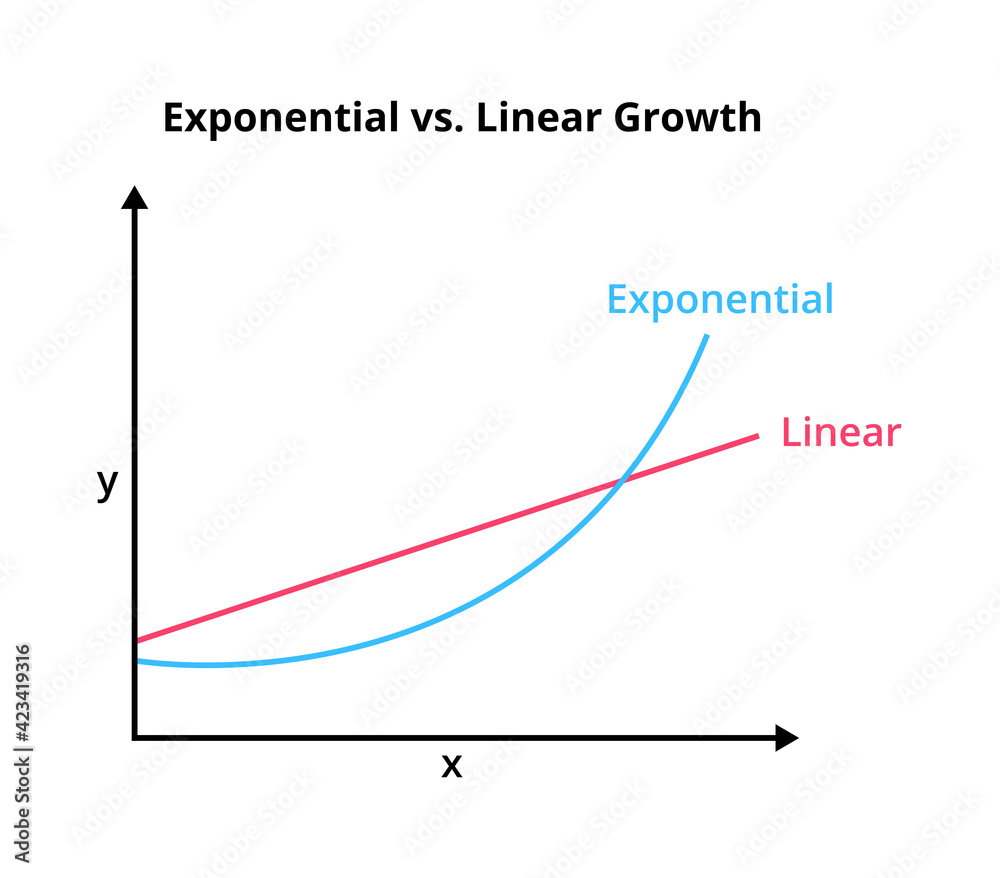
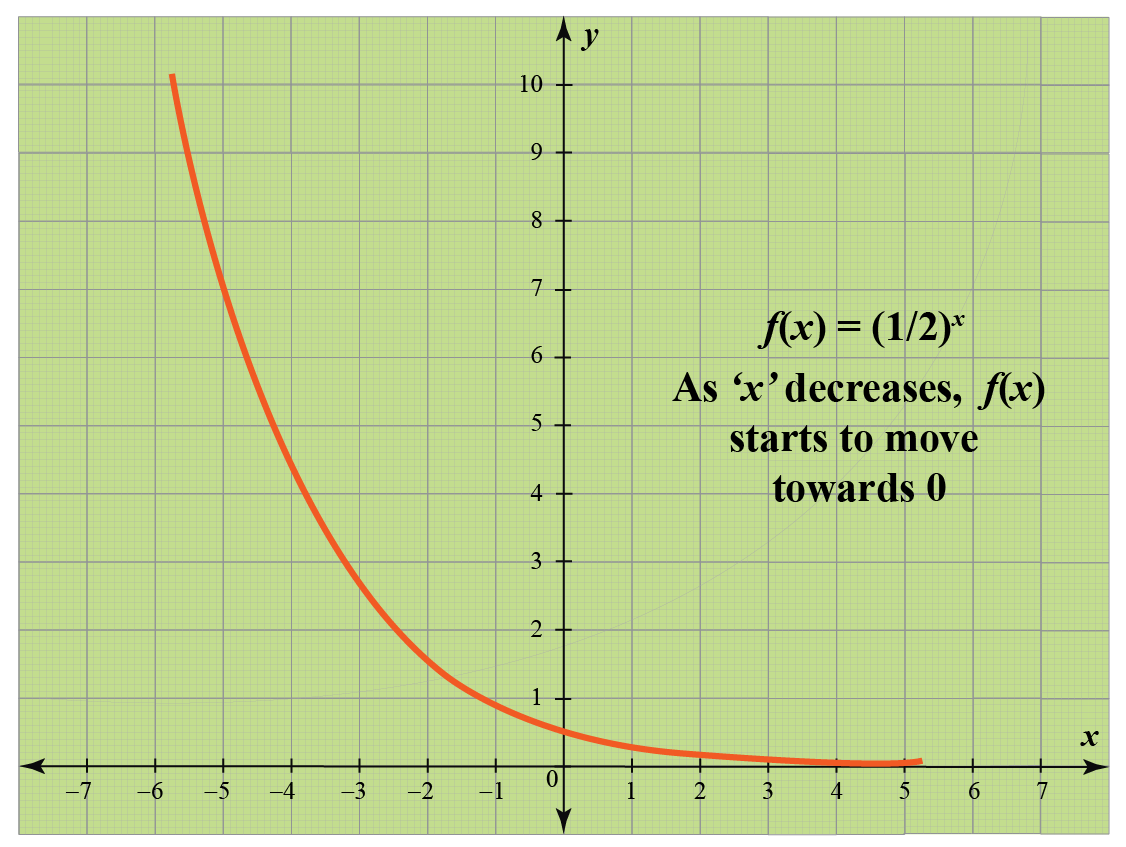
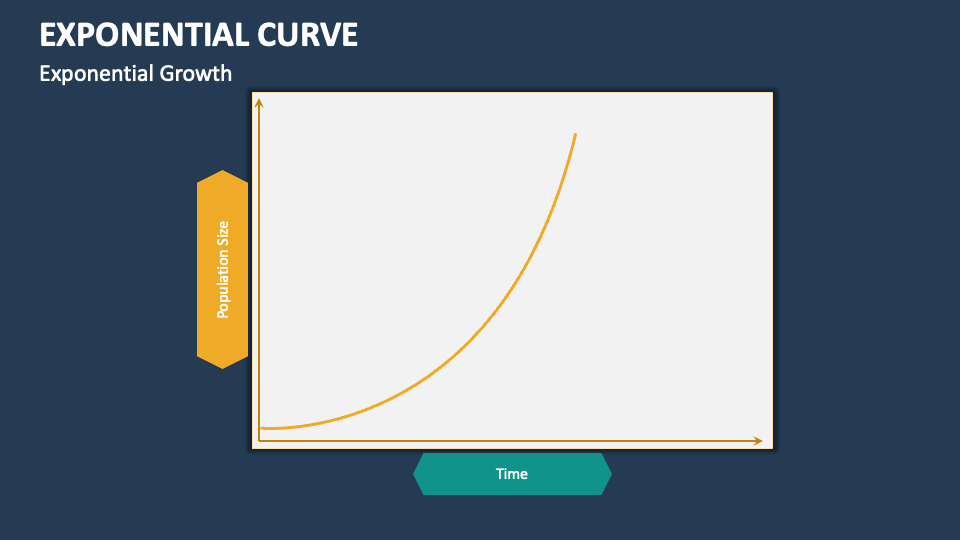
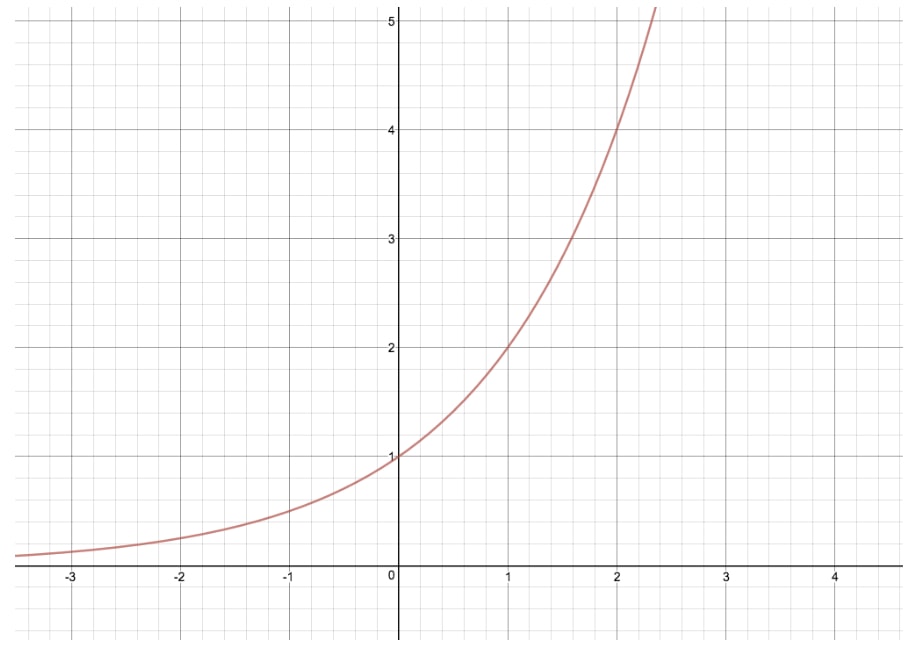
Are curved lines exponential. We'll see that an exponential function has a horizontal asymptote in one direction and rapidly changes in the other direction. Exponential growth produces a curved line on a graph, reflecting the increasing rate of change. Recall the table of values for a function of the form \(f(x)=b^x\) whose base is greater than one.

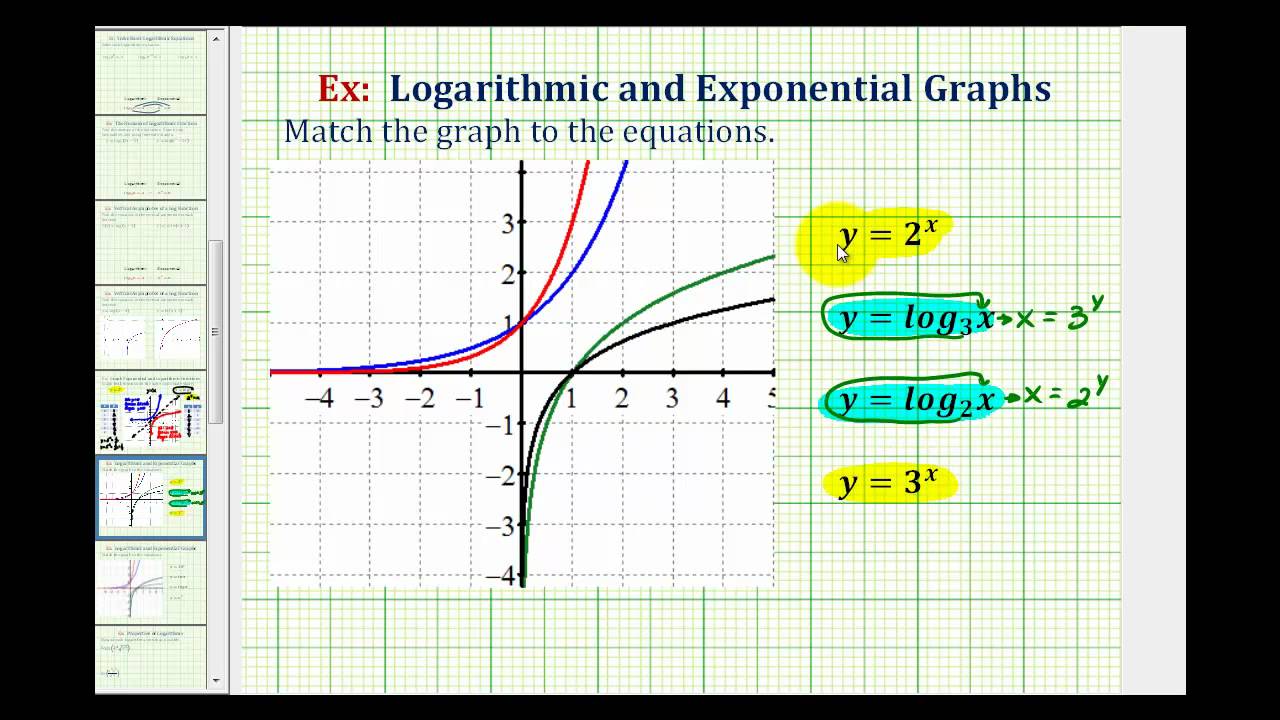
Here’s what i focus on: We’ll use the function \(f(x)=2^x\). Graph exponential functions and their transformations.

An exponential function is defined as a function with a positive constant other than \(1\) raised to a variable exponent. You probably noticed the curvy line on the original graph turned into a straight line on the log transformed graph. The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value.

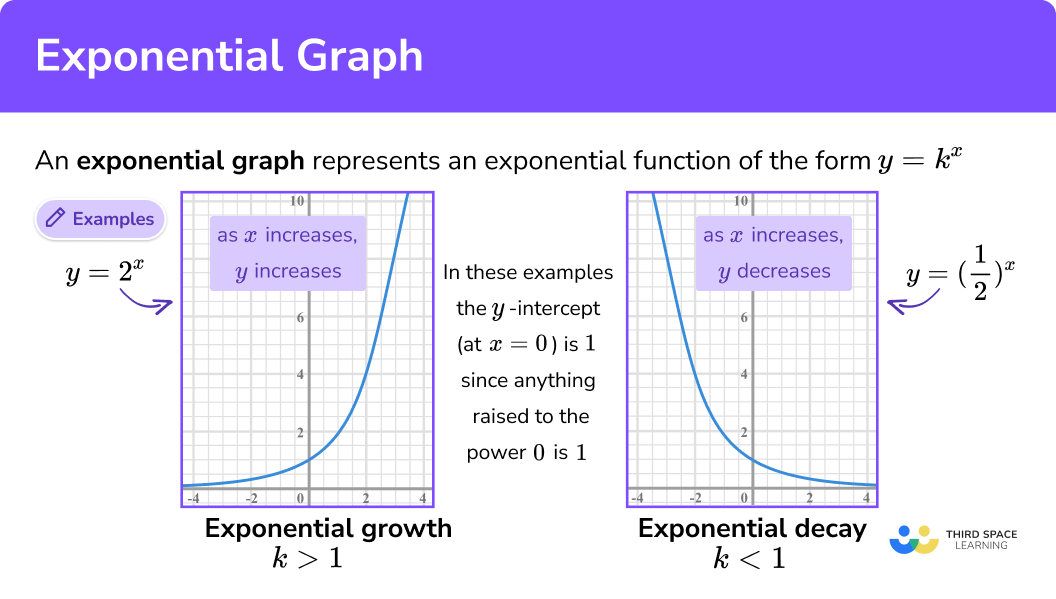
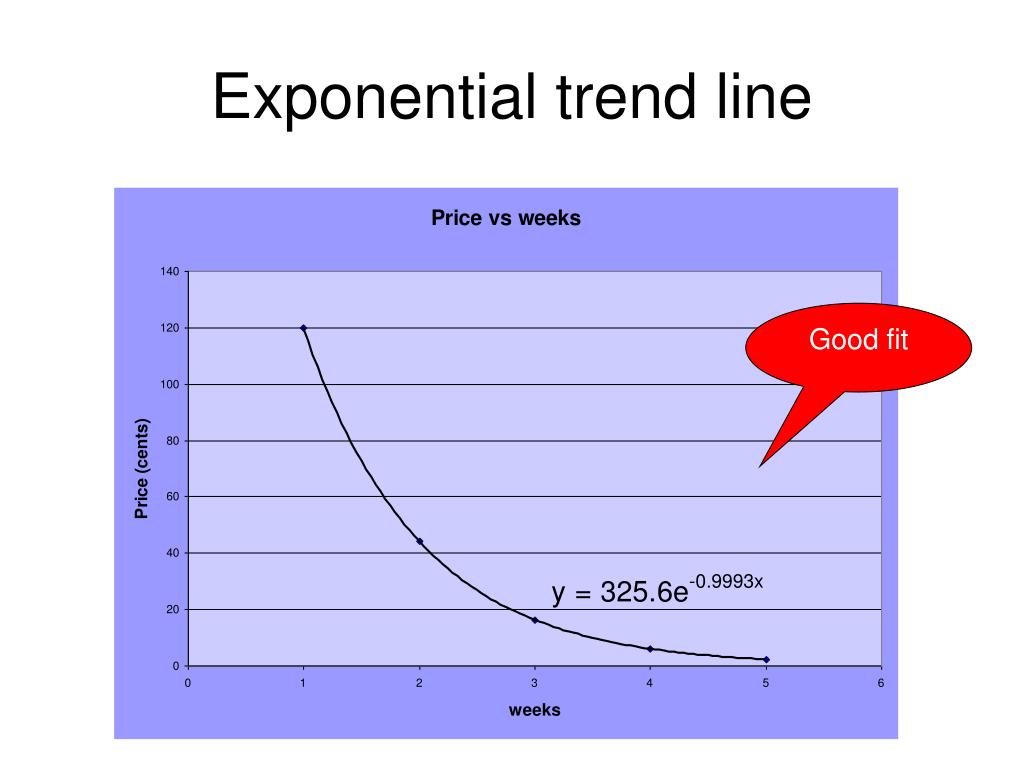
An exponential graph is a curve that has a horizontal asymptote and it either has an increasing slope or a decreasing slope. The curvy line turned into a straight line! An exponential model can be found when the growth rate and initial value are known.

Want to join the conversation? In this lesson, we'll learn to: Identify the features of exponential functions.

How do you tell if a relationship is linear or exponential? The red curve is the exponential function. Connect the points as best you can, using a smooth curve (not a series of straight lines).

By definition, an exponential function has a constant as a base and an independent variable as an exponent. How do i graph exponential functions, and what are their features? The exponential curve depends on the exponential function and it depends on the value of the x.

Thus, \(g(x)=x^3\) does not represent an exponential function because the base is an independent variable. An exponential function is a function that grows or decays at a rate that is proportional to its current value. Before we begin graphing, it is helpful to review the behavior of exponential growth.

In real life, every time 12 hours passes, the bacteria increase by a factor of 10. Graphing exponential functions. Use the shape of an exponential graph to help you:

Curve in graph: It takes the form of. (i) when \ (a>1,\) the graph strictly increases as \ (x.\)