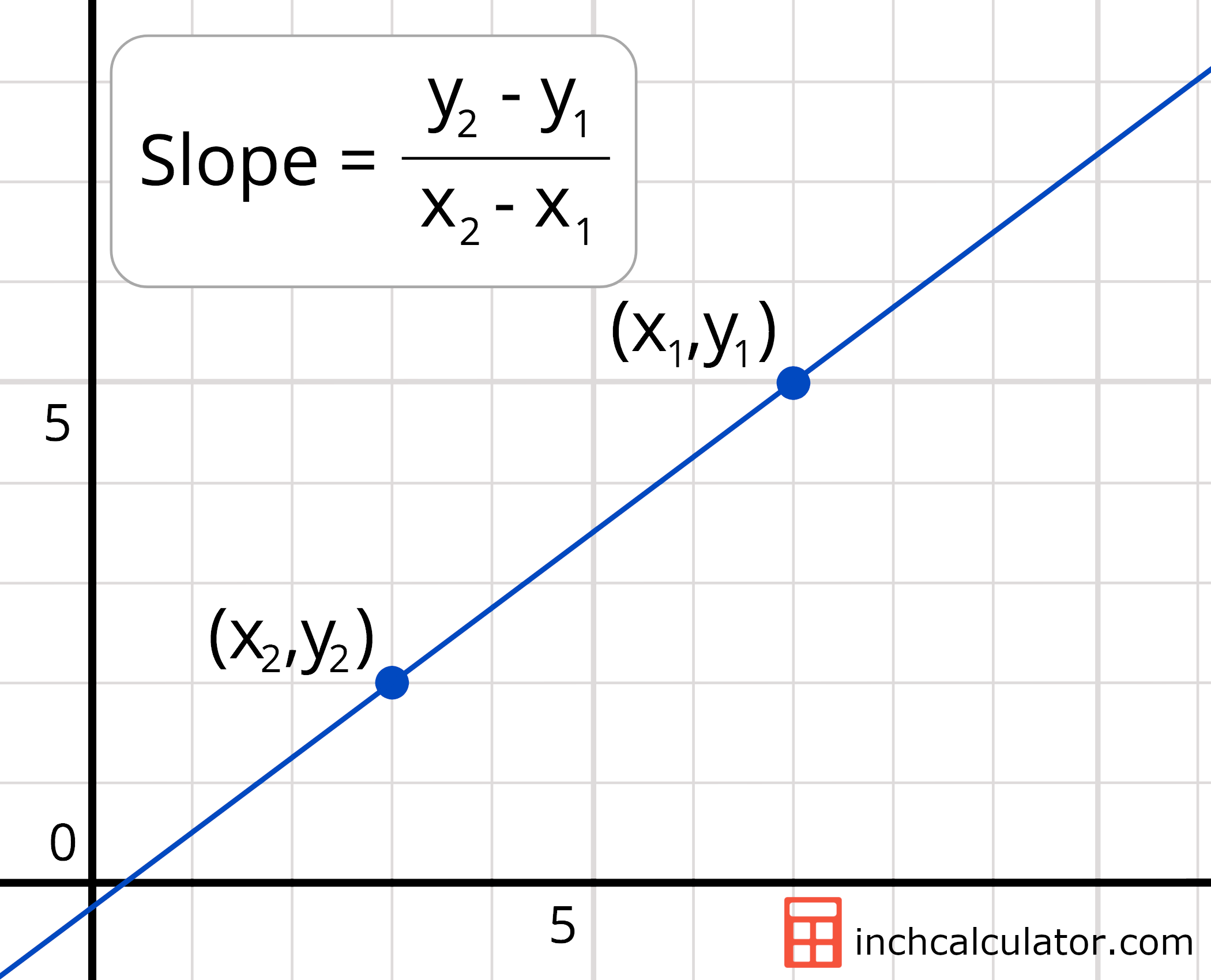Fantastic Info About How Do You Determine Which Slope Is Greater To Make A Continuous Line Graph In Tableau

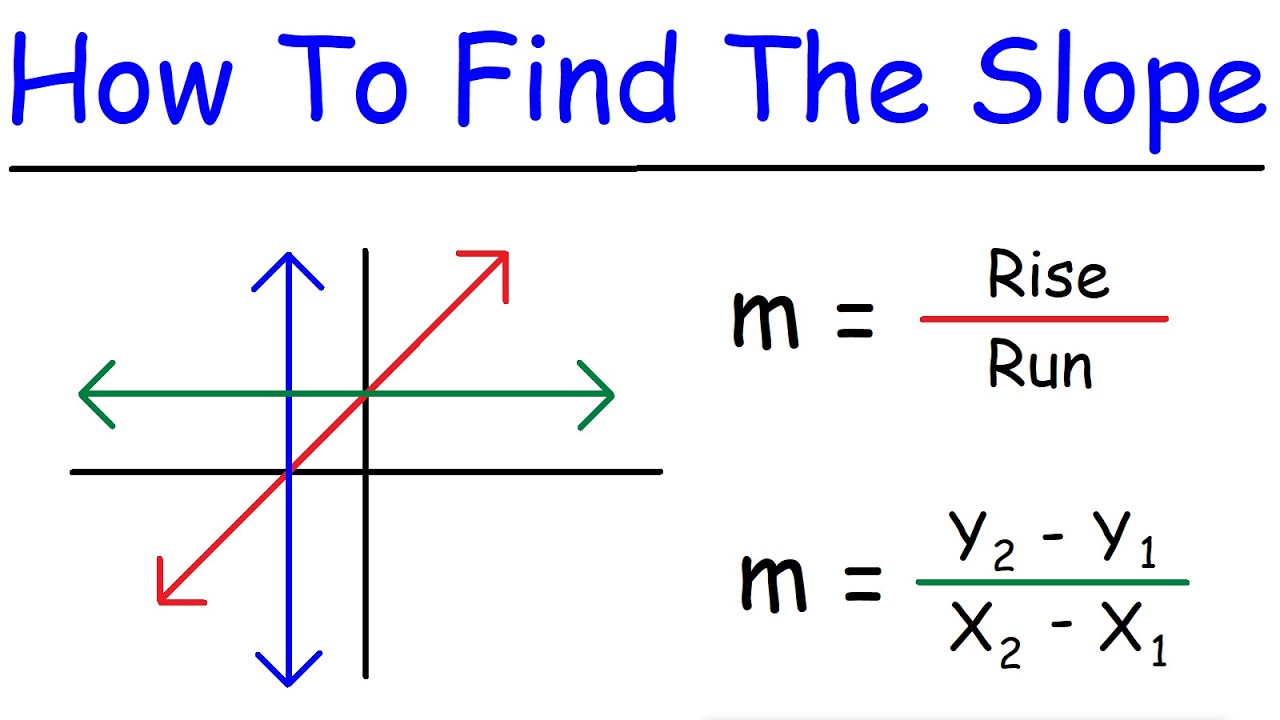
But i just like to think of it as rise over run.

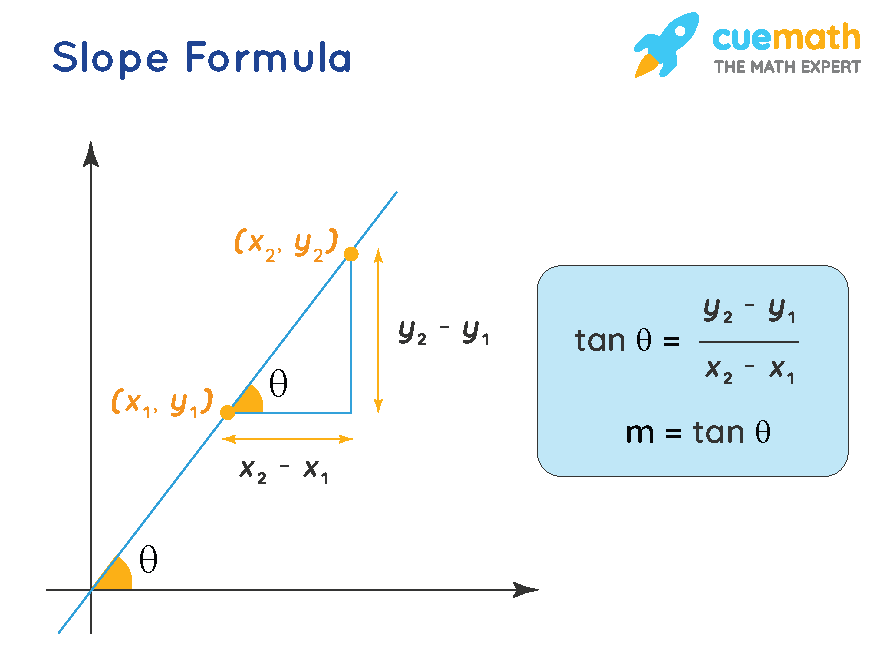
How do you determine which slope is greater. An argument for the steep slope being greater goes like this: Learn how to write the slope formula from scratch and how to apply it to find the slope of a line from two points. The steepness and direction of a line.

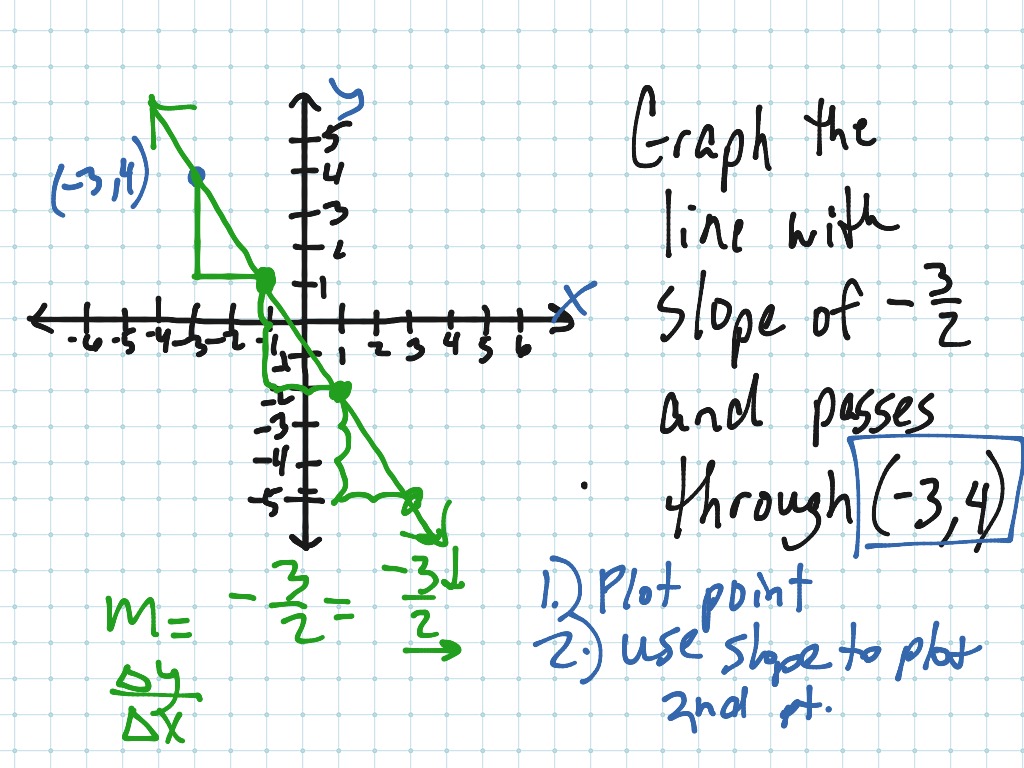
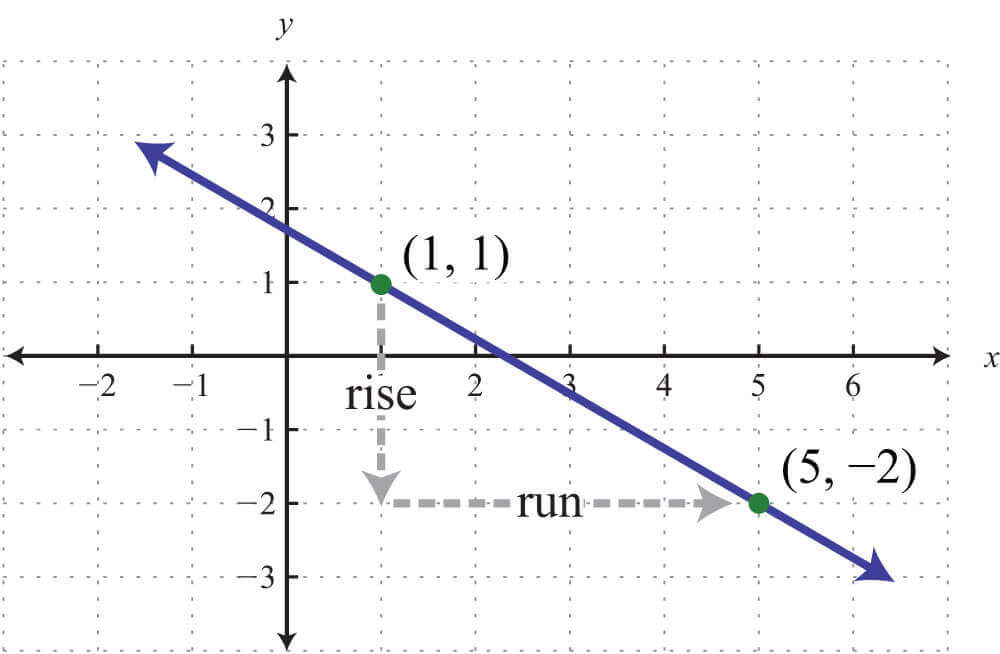
To find the slope of the line, pick two points on the line. If you have a negative slope. For an example, we take two lines l1 and l2.

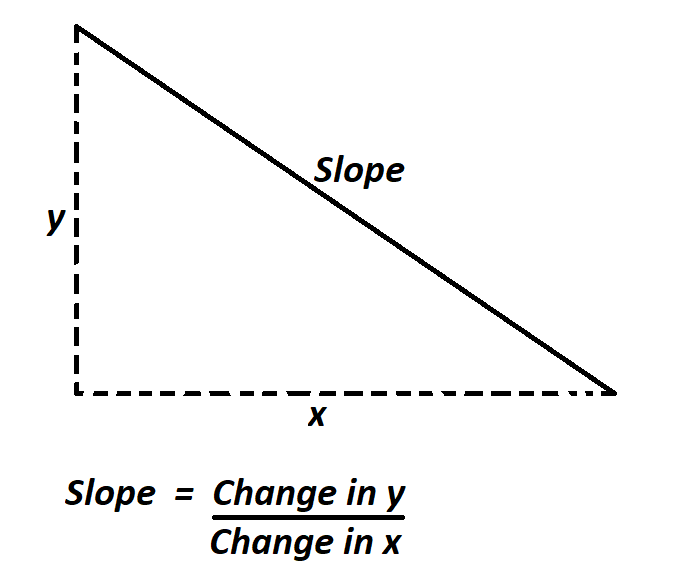
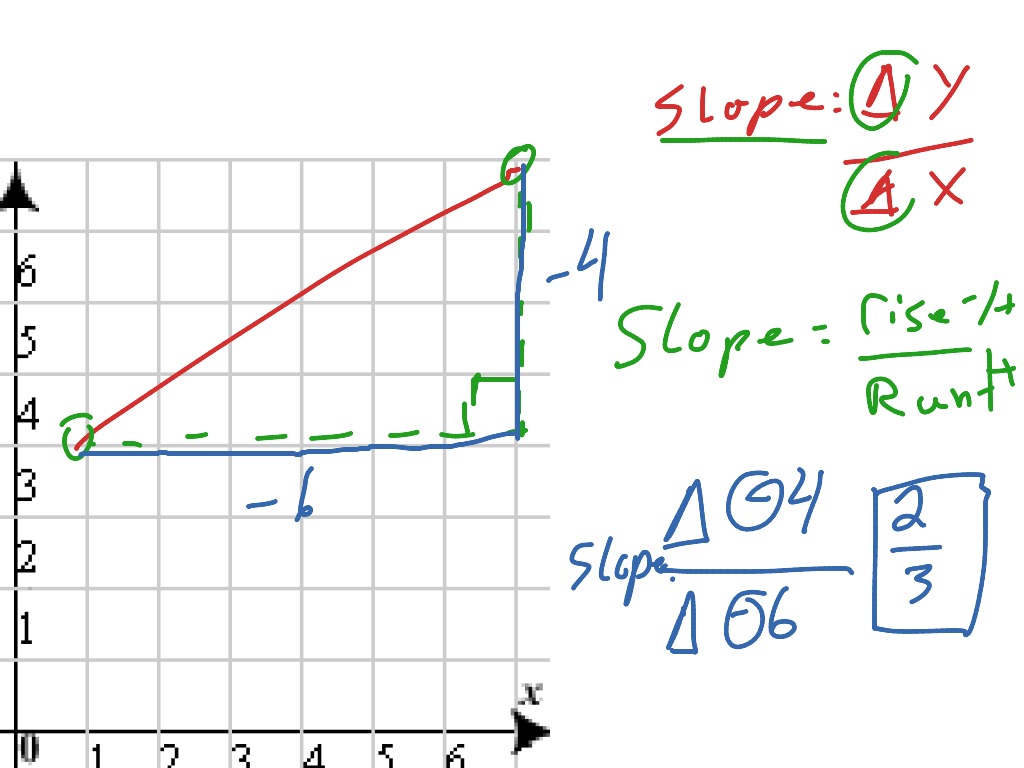
The steeper it is, the bigger the slope. Here's a rough sketch of the graph, and we want to determine which line has the steeper slope. Divide the change in height by the change in horizontal distance.

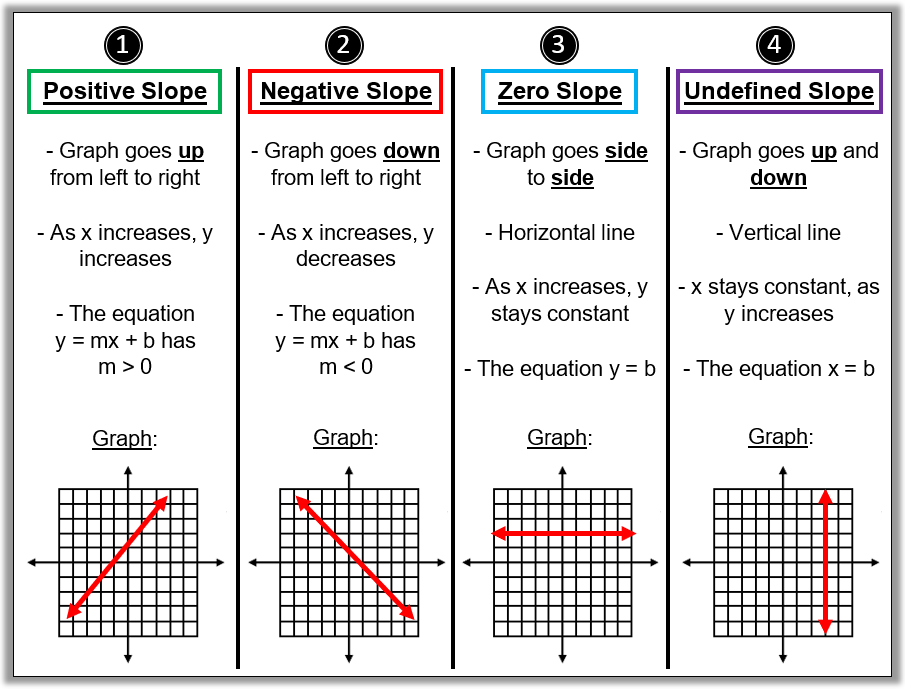
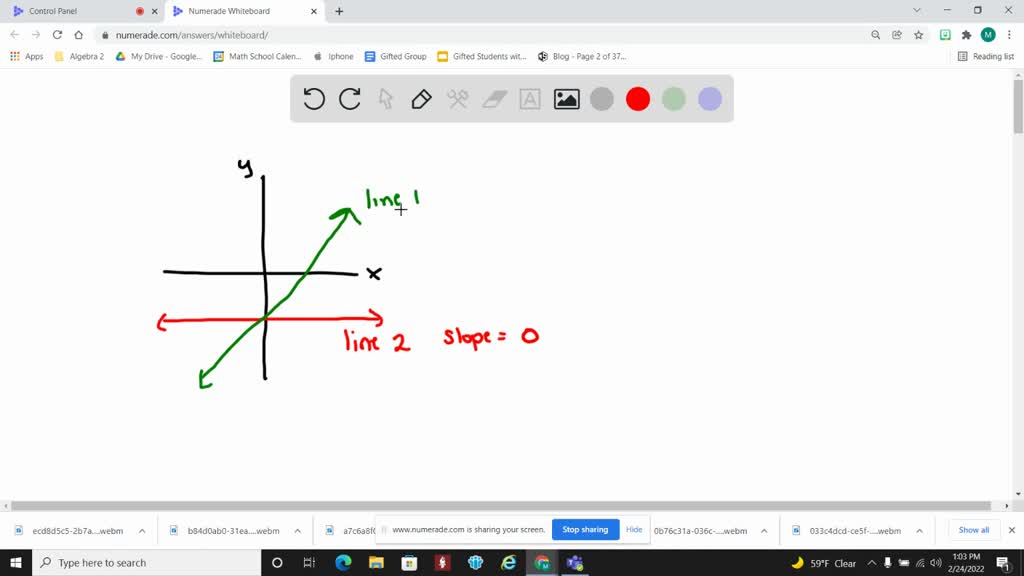
We would like to show you a description here but the site won’t allow us. Line two is going down from left to right, which means it has a negative slope. So because both lines are going up to the right, they both have a positive slope.

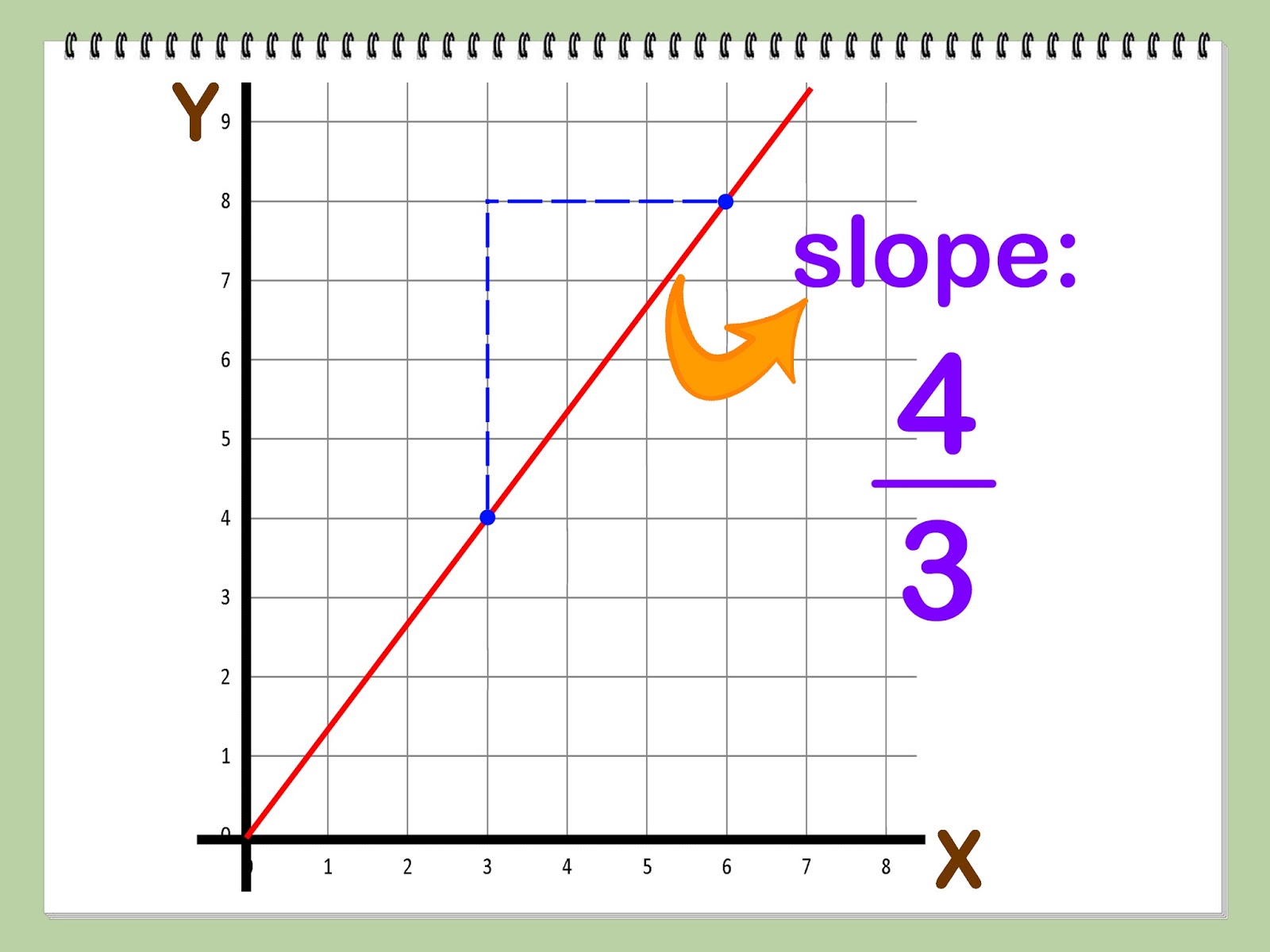
Find the slope of a line from its graph. It may be given in terms of the angle of elevation. The line with slope 4 is steeper than the line with slope 1/2.

So if you look at line one, you'll notice that it goes up. It would be quite odd for the slopes two upper sides on an equilateral triangle to switch greaterness after the triangle is flipped around the center of the base. The gradient (also called slope) of a line shows how steep it is.

To predict whether the lines are parallel or perpendicular or at any angle without using any geometrical tool, the best way to find this is by measuring the slope. Line one is going up from left to right, which means it has a positive slope. It's kind of annoying to have to draw a graph every time we want to.

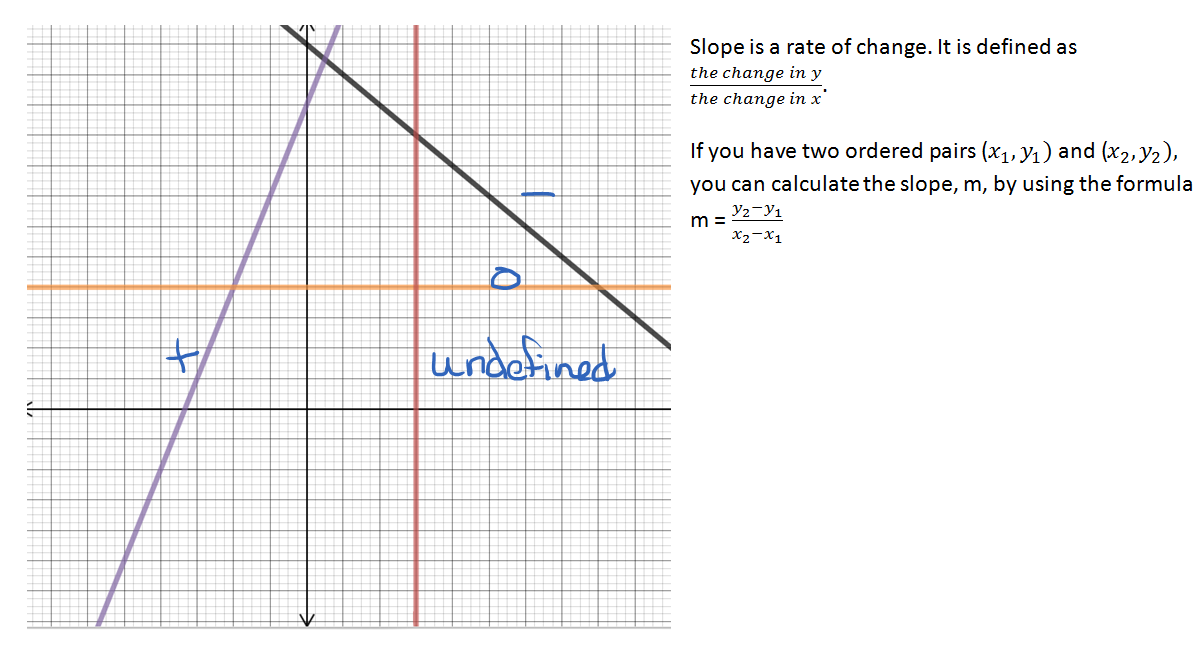
Find the slope of horizontal and vertical lines. In technical terms, the slope of the line is the change in y over the change in x. A very high positive slope, as x increases, y is going to increase fairly dramatically.

A line that's flat has a slope of 0. This elevation grade calculator determines and expresses, in four different ways, the slope of an earthen surface. As x increases, your y is actually going to decrease.